[BOJ]12015. 가장 긴 증가하는 부분 수열 2

12015. 가장 긴 증가하는 부분 수열 2

Longest Increasing Subsequence Size

이분 탐색을 이용하면 최장 증가 부분 수열(이하 LIS)을 O(nlogn)의 시간복잡도로 구할 수 있다.

현재 가지고 있는 숫자 리스트를 LIST, LIS의 길이를 계산하기 위해 이용되는 빈 리스트를 lis라고 하자. 방법은 다음과 같다.

1. LIST의 첫 번째 원소를 lis에 추가한다.
2. LIST의 원소 num은 다음 규칙을 따른다.
   1. num이 LIST[-1]보다 큰 경우 lis의 맨 뒤에 추가한다.
   2. 그렇지 않은 경우 lis에서 같는 lower bound를 찾고 그 위치에 갱신한다.
      1. 이때 lower bound를 찾기 위해 이분 탐색이 사용된다.

# 현재 가지고 있는 숫자 리스트
LIST = list(map(int, sys.stdin.readline().split()))

# 가장 긴 증가하는 부분 수열 리스트
# LIST의 첫번째 원소를 추가한다
lis = [LIST[0]]

for num in LIST[1:]:
    # 만약 현재 lis의 마지막 숫자보다 크다면 맨 뒤에 추가한다
    # 즉 이때 무조건 LIS의 길이는 증가한다
    if lis[-1] < num:
        lis.append(num)

    # 현재 숫자의 위치를 이분 탐색을 통해 찾고 그 위치에 넣는다
    else:
        idx = binary_search(lis, num)
        lis[idx] = num

이 과정이 완료된 후 lis 리스트의 크기가 최장 증가 부분 수열의 길이가 된다. 즉 lis 리스트는 최장 증가 부분 수열이 아니며 그 길이만 동일한 것이다. 이때 lis 리스트의 내부 원소가 다른데 길이만 동일하다는 부분이 헷갈려 여러 설명을 찾아보았고 다음 유투브 강의를 통해 이해할 수 있었다.

Longest Increasing Subsequence O(n log n) dynamic programming Java source code

해당 강의는 Patience 게임을 통해 알고리즘을 설명하고 있다. 강의에서 등장하는 Patience 게임은 자신의 카드를 곂쳐 내려놓아 최소한의 카드 덱을 만드는 것을 목표로 한다. 카드를 내려놓는 규칙은 위 코드와 동일하다.

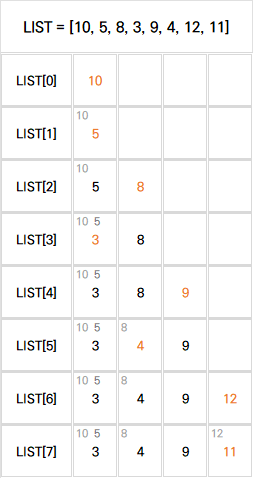
다음과 같은 숫자 카드가 있을 때 내려놓는 순서와 결과적으로 만들어지는 카드덱은 다음과 같다. 곂쳐져 보이지 않는 카드는 상단에 표시해두었다. (아래 표는 강의의 그림을 재구성한 것이다.)

마지막 원소까지 탐색한 뒤 나오는 결과 [3, 4, 9, 11] 리스트는 lis 리스트의 결과와 동일하다.

lis 리스트는 최종 LIS를 구하는 것이 아니라 최종 LIS를 구하기 위한 최적의 카트 덱 리스트를 기록하는데 목적이 있다. 이 부분을 착각하여 알고리즘을 제대로 이해하지 못했었다. 즉, [3, 4, 9, 11] 리스트는 이후 추가될 새로운 여덟 번째 원소에 대비하여 준비된 리스트인 것이다. 하지만 여덟 번째 원소는 없기 때문에 여기서 종료된다.

code

import sys


def binary_search(cur_lis, target):
    # 현재 lis에서 목표 숫자가 들어갈 수 있는 자리 즉,
    # lower bound를 반환하는 함수

    left = 0
    right = len(cur_lis)
    while left <= right:
        mid = (left + right) // 2
        if target < cur_lis[mid]:
            right = mid - 1
        elif cur_lis[mid] < target:
            left = mid + 1
        else:  # l[mid] == target
            return mid

    return left


N = int(sys.stdin.readline())
LIST = list(map(int, sys.stdin.readline().split()))

lis = [LIST[0]]  # 가장 긴 증가하는 부분 수열 리스트

for num in LIST[1:]:
    # 만약 현재 lis의 마지막 숫자보다 크다면 맨 뒤에 추가한다
    # 즉 이때 무조건 LIS의 길이는 증가한다
    if lis[-1] < num:
        lis.append(num)

    # 현재 숫자의 위치를 이분 탐색을 통해 찾고 그 위치에 넣는다
    else:
        idx = binary_search(lis, num)
        lis[idx] = num
print(len(lis))  # 길이 출력

요약

이분탐색을 이용하여 O(nlogn)의 시간복잡도로 LIS를 구할 수 있다. 이 과정 중에는 항상 최적의 LIS를 구할 수 있도록 원소들을 재정렬해 기록하는 빈 리스트가 필요하며 이 리스트의 최종 모습은 LIS와 동일하지 않을 수 있다.