[BOJ]3663. 고득점

3663. 고득점

❌code1

def solution(name):
    answer = 0

    # 검사된 인덱스를 기록하는 비트 마스킹
    # 0번 인덱스에서 시작되므로 초깃값으로 (1 << 0)을 갖는다
    initial_bit_mask = 1
    for i, v in enumerate(name):
        # 각 인덱스의 알파벳을 만들기 위해 필요한 동작 횟수 추가
        answer += min(ord(v) - ord('A'), abs(ord(v) - ord('Z') - 1))

        # A는 검사할 필요가 없으므로 이미 검사되었다고 표시
        if v == 'A':
            initial_bit_mask |= 1 << i

    # A를 제외한 모든 알파벳을 검사하는데 필요한 최소 동작 횟수
    # 최댓값은 문자열의 길이이므로 이를 초깃값으로 설정
    min_move = len(name) - 1

    # 모든 동작을 (현재 인덱스, 동작 횟수, 비트 마스킹) 양식으로 저장할 리스트
    move_list = [(0, 0, initial_bit_mask)]  # 초깃값 추가

    while move_list:
        # 현재 인덱스, 동작 횟수, 비트 마스킹
        cur_idx, move_cnt, bit_mask = move_list.pop()

        # 만약 현재까지의 동작 횟수가 최솟값보다 크거나 같다면 더이상 탐색할 필요 없음
        if min_move <= move_cnt:
            continue

        # 만약 현재 모든 인덱스가 탐색된 경우 정답에 최솟값 갱신
        if bit_mask == (1 << len(name)) - 1:
            min_move = min(min_move, move_cnt)

        # 현재 인덱스에서 한 칸 전진하는 경우(인덱스 증가)
        move_list.append(
            (
                (cur_idx + 1) % len(name),
                move_cnt + 1,
                bit_mask | (1 << ((cur_idx + 1) % len(name)))
            )
        )

        # 현재 인덱스에서 한 칸 후진하는 경우(인덱스 감소)
        if cur_idx == 0:
            move_list.append(
                (
                    len(name) - 1,
                    move_cnt + 1,
                    bit_mask | (1 << (len(name) - 1))
                )
            )
        else:
            move_list.append(
                (
                    cur_idx - 1,
                    move_cnt + 1,
                    bit_mask | (1 << (cur_idx - 1))
                )
            )

    answer += min_move
    return answer


T = int(input())
for _ in range(T):
    print(solution(input()))

시도

알파벳을 원하는 알파벳으로 바꾸는데 필요한 상하 동작은 모든 경우에 대해 동일하므로 이를 미리 처리한다. 좌우 이동 동작을 처리하기 위해서 모든 경우의 수를 탐색한다.

각 인덱스에 대하여 좌측으로 한 칸 이동, 우측으로 한 칸 이동이 가능하며 인덱스 범위를 벗어나는 경우 원형으로 움직이도록 다음 인덱스를 조정한다. 모든 동작을 리스트에 저장하여 문제에서 요구하는 경우가 등장할 시 최소 이동 횟수를 갱신한다.

모든 동작은 (현재 인덱스, 동작 횟수, 비트 마스킹) 양식으로 기록하며 비트 마스킹은 A가 아닌 알파벳이 탐색 되었는지 여부를 기록한다. 이를 위해 A를 나타내는 인덱스는 시작점 0번 인덱스와 함께 이미 탐색이 완료되었다고 초깃값을 설정한다. 만약 동작 횟수가 최소 동작 횟수를 넘어가는 경우 해당 동작에 대해서는 좌우 이동을 탐색하지 않는다.

문제

시간 초과.

⭕code2

def solution(name):
    answer = 0
    length = len(name)  # name의 길이

    for letter in name:
        # 각 인덱스의 알파벳을 만들기 위해 필요한 동작 횟수 추가
        answer += min(ord(letter) - ord('A'), abs(ord(letter) - ord('Z') - 1))

    # A를 제외한 모든 알파벳을 검사하는데 필요한 최소 동작 횟수
    # 최댓값은 문자열의 길이이므로 이를 초깃값으로 설정
    min_move = length - 1
    for i in range(length):
        next_i = i + 1  # 현재 알파벳 이후로 처음 만나는 A가 아닌 알파벳의 인덱스
        while next_i < length and name[next_i] == 'A':
            next_i += 1

        # 이동할 수 있는 경우의 수 1. 우측 -> 좌측
        # 이동할 수 있는 경우의 수 2. 좌측 -> 우측
        min_move = min(min_move, i + (i + length - next_i), 2 * (length - next_i) + i)

    answer += min_move
    return answer


T = int(input())
for _ in range(T):
    print(solution(input()))

시도

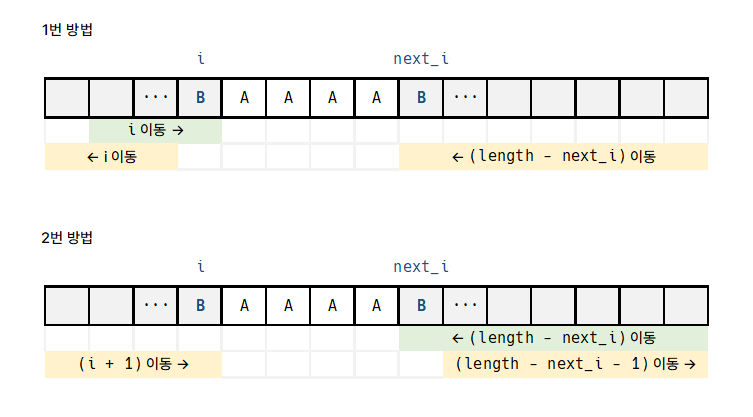
인덱스 i에서 좌측으로 이동 중 A를 만나면 A가 연속되는지 확인한 후 연속된 A가 끝나는 지점 즉, A가 아닌 알파벳이 등장하는 인덱스 next_i를 기록한다. 이때 모든 인덱스에 대하여 A를 제외한 모든 알파벳을 원하는 값으로 바꾸기 위해 이동할 방법은 2가지이다.

1. 0에서 i까지 우측으로 이동한 후, 좌측으로 다시 돌아가 next_i에 도달한다.
2. 0에서 next_i까지 좌측으로 이동한 후, 우측으로 다시 돌아가 i에 도달한다.

두 방법을 모든 인덱스에 대하여 적용한 뒤 그 중 최솟값을 구한다.

요약

원형으로 이동할 수 있는 리스트에서 특정 값을 방문할 때 경우의 수는 2가지이며 이 방법을 모든 인덱스에 대해 적용하여 최소 이동 횟수를 구할 수 있다.